UC BerkreyのPachter (2011)によるRNA-seqデータ定量モデルの総括的な論文をトレースしながら、基礎的なトピックを拾いつつ、数理的背景をひととおり把握できるよう、ライトタッチにまとめてみた。ちなみに、edgeRやDESeqなどいわゆるカウント派の手法（トピックとしては過分散や一般化線形モデルあたり？）については解説していない。

リードカウントで発現定量を行う際の問題点

以下の図は、Cole et al. (2013)の論文よりの引用。これがリードカウント発現定量の問題点をよくあらわしている。要するに、知るべきなのはRNAからとれるリードの数でなく、RNAの本数であるということである。

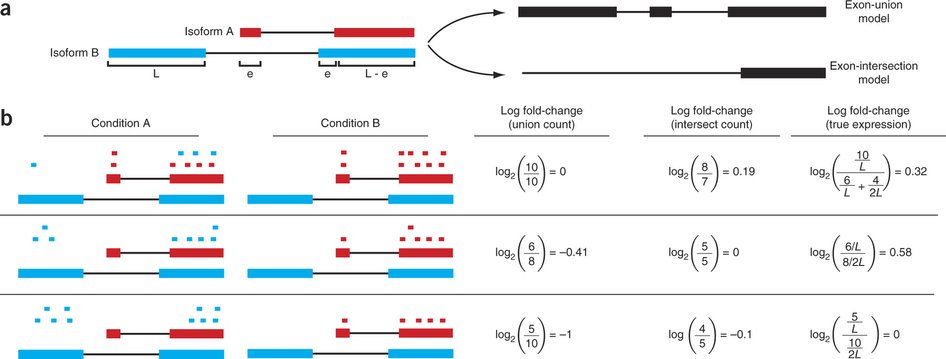
カウント定量の問題点

すなわち、RNAの本数を推定するには、検出リード数を長さで規格化することが（詳細は以下に見ていくように）良い方法である。ちなみに、現在主流の発現変動遺伝子(DEG)解析手法であるedgeRやDESeqは、isoformを区別せずに1遺伝子単位のunionカウント（上図参照）をとったものをスタートの定量値として想定しているようである。つまり、同一遺伝子の異なるサンプル間の発現変動のみに着目することで、上記の長さ問題の回避を図っている（同じ遺伝子同士ならバイアスも同じだという理屈）。しかし、それだけではまだ問題は回避できていない。例えば簡単な例として、同じ遺伝子について、isoformを区別せず、サンプルAとサンプルBで遺伝子単位でRNAの総量（総本数）が変わらないとしても、例えばその内訳として長いisoformと短いisoformが2:3から3:2になるだけで、サンプルAおよびBでとれるタグ数は変わってしまい、発現変動を起こしたように見えてしまう（マイナーな問題なのかもしれないが）。こういった視点から、上記Coleらの論文ではisoformが交代するというシナリオのもと、シミュレーションデータを交えて議論されている。

RNA-seqデータ生成モデルの基本形

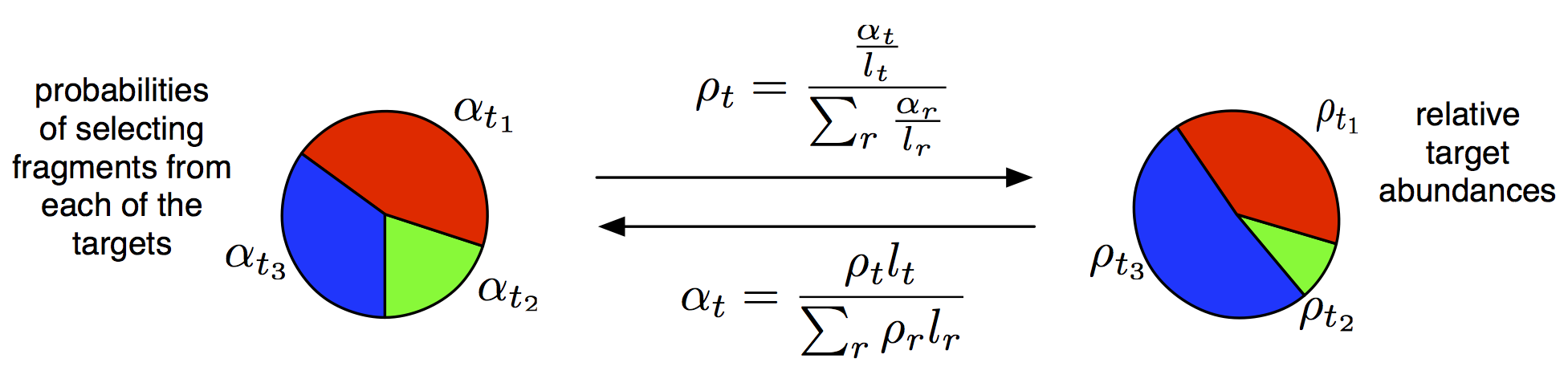
シーケンスされた配列断片（リード）$f \in F$の集まり（データ）から、転写産物$t \in T$の濃度を表す相対量$\rho_t$を知ることが当面の目的である。ここで相対量とは検出した全mRNA中のある転写産物$t$の（個数の）割合という意味であり、$\sum_{t \in T}{\rho_t} = 1$とする1。

以下の条件で、まず最も単純なモデルの定式化から出発する。

  • Single-endである
  • リードのマルチヒットは存在しない
  • リードの長さ(cycle数)＝フラグメント長でありすべてが同じ長さ$m$
  • ほか、ひとまずいろんなbiasのことは考えない

つまり、すべて同じ長さのシングルリードの山があり、各々の3’-endは必ずひとつの転写産物のひとつの位置に対応している…といった状況を考える。後の都合がよいので以降は暗黙の仮定として、常にリードの3’-endの位置を基準に考える。先に進むなかで、この単純なモデルの制約をゆるめつつ現実のデータに即したモデルにしていく。

ある１つのリードが転写産物$t$のものである確率

転写産物$t$にマップされるリードの部分集合を$F_t \subseteq F$とする。ひとつのリード$f$を取得したとき、それが転写産物$t$のものである確率（$t$の取得確率）を考えてみる。

\[\begin{equation} \alpha_t := \mathrm{P}(f \in F\_t) = \frac{\rho\_t \tilde{l}\_t}{\sum_{r \in T} \rho\_r \tilde{l}\_r} \label{defa} \end{equation}\]

ここで、$\tilde{l}_t=l_t-m+1$は$t$の実効長であり、長さ$l_t$を持つ転写産物$t$から取得可能なリード3’-endの位置の総数をあらわしている2。この$\alpha_t$は、潜在的に取得可能なすべての転写産物の総実効長のうち、転写産物$t$だけの総実効長$\rho_t \tilde{l}_t$が占める割合だと考えれば分かりやすい。

データの尤度

ある$f$について、対応する$t$が決まっているとき、その実効長のうち$i$番目が選ばれる条件付き確率は、$1/\tilde{l}_t$である（どの場所でも同じ確率）。したがって、特定の1つのリード3’-endが、特定の位置$i$へマッピングされる同時確率は以下となる。

\[\begin{equation} \mathrm P(i, f \in F_t) = \mathrm P(f \in F_t) \cdot \mathrm P(i \mid f \in F_t) = \alpha_t \cdot \frac{1}{\tilde{l}_t} \end{equation}\]

この特定の1つのリードが得られる確率を元にして、パラメータ $\boldsymbol\alpha= (\alpha_1,\alpha_2,\ldots,\alpha_{|T|})$が与えられた時のすべてのリード$F$が得られる確率をあらわす尤度関数をつくる。

\[\begin{equation} \mathcal{L}(\boldsymbol\alpha) = \prod_{t \in T} \prod_{f \in F_t} \left( \frac{\alpha_t}{\tilde{l}_t}\right) = \prod_{t \in T} \left( \frac{\alpha_t}{\tilde{l}_t}\right)^{X_t} \label{eq:likfun} \end{equation}\]

ここで、 $X_t=|F_t|$とした。この対数線形モデルの形をした尤度関数$\mathcal{L}$を最大化するパラメータ$\hat{\boldsymbol\alpha}_{ML}=(\hat\alpha_1,\hat\alpha_2,\ldots,\hat\alpha_{|T|})$は解析的に容易に求められる。

\[\begin{equation} \max_{\boldsymbol\alpha} \mathcal{L(\boldsymbol\alpha)} \quad s.t. \ \sum_{t \in T}{\alpha_t} = 1 \end{equation}\]

ラグランジュの未定乗数法で解析的に解く

対数尤度関数に制約条件の項を加えた関数$L’(\boldsymbol\alpha,\lambda)$の極値を求める。

\[\begin{eqnarray} \mathcal{L(\boldsymbol\alpha)} &\propto& \prod_{t \in T} \alpha_t^{X_t}\\ \log \mathcal{L(\boldsymbol\alpha)} &\propto& \sum_{t \in T} X_t \log \alpha_t \\ L'(\boldsymbol\alpha,\lambda) &=& \sum_{t \in T} X_t \log \alpha_t + \lambda \left(\sum_{t \in T} \alpha_t - 1\right)\\ \frac{\partial L'}{\partial \alpha_t} &=& \frac{X_t}{\alpha_t} + \lambda = 0 \\ -\lambda \alpha_t &=& X_t \label{eq:alpha} \\ -\lambda \sum_{t \in T} \alpha_t &=& \sum_{t \in T} X_t \\ -\lambda &=& N \label{eq:lambda} \end{eqnarray}\]

ここで、$N$は総リード数とした。最後に、式($\ref{eq:lambda}$)で求めた$\lambda$を式($\ref{eq:alpha}$)に代入すれば、

\[\begin{equation} \hat{\alpha_t} = \frac{X_t}{N} \label{eq:alphamle} \end{equation}\]

として、$\boldsymbol\alpha$の最尤推定量が解析的に得られる。つまり、あるリード$f$をひとつピックアップしたとき、トータルリード数のうち各々の転写産物$t$由来のリード数の占める割合$X_t/N$が、各々の転写産物$t$に当たる確率$\alpha_t$であることが尤もらしい…と解釈できる（あたりまえの帰結）。

$\alpha_t$と$\rho_t$の関係

ただ、そもそも知りたかったのは取得確率$\alpha_t$ではなかった。そこで、転写産物$t$の相対量$\rho_t$と取得確率$\alpha_t$の関係を明らかにしておく必要がある。式($\ref{defa}$)より、

\[\begin{eqnarray} \frac{\alpha_t}{\tilde{l}_r} \sum_{r \in T} \rho_r \tilde{l}_r &=& \rho_t \label{eq:rhoalpha}\\ \sum_{r \in T} \frac{\alpha_t}{\tilde{l}_r} \sum_{r \in T} \rho_r \tilde{l}_r &=& \sum_{r \in T} \rho_t = 1 \\ \sum_{r \in T} \rho_r \tilde{l}_r &=& \left( \sum_{r \in T} \frac{\alpha_t}{\tilde{l}_r} \right)^{-1} \label{eq:rholsum} \end{eqnarray}\]

あとは式($\ref{eq:rholsum}$)の結果を式($\ref{eq:rhoalpha}$)に戻せば、以下の関係式を得ることができる。

\[\begin{equation} \label{eq:inverserho} \rho_t \quad = \quad \frac{\frac{\alpha_t}{\tilde{l}_t}}{\sum_{r \in T} \frac{\alpha_r}{\tilde{l}_r} } \end{equation}\]

これは、すべての転写産物の取得確率の（実効長の逆数による）重み付きの和のうち、ひとつの転写産物$t$の重み付きの取得確率の占める割合が$\rho_t$であると解釈できる。以下のトピックで、「重み」とはなんだったかに納得がいくはずである。

$\rho_tと$\alpha_t$の関係　

$\rho_t$の最尤推定量はRPKMの定数倍

式($\ref{eq:inverserho}$)の関係使って、ようやく一番知りたかった転写産物$t$の相対量$\rho_t$をすでに最尤法で求めた$\alpha_t$の最尤推定量($\ref{eq:alphamle}$)と引き換えることができる。

\[\begin{eqnarray} \hat{\rho}_t & = & \frac{X_t}{N \tilde{l}_t} \left( \sum_{r \in T} \frac{X_r}{N\tilde{l}_r} \right)^{-1} \label{eq:rhomle}\\ & \propto & X_t \cdot \frac{10^3}{\tilde{l}_t} \cdot \frac{10^6}{N} = RPKM_t \label{eq:rpkm} \end{eqnarray}\]

式($\ref{eq:rhomle}$)の最尤推定量においても、重みというのはやはり実効長の逆数（長さペナルティ）である。$N$やほかの$t$に依存しない部分は$\sum \hat\rho_t = 1$になるよう調整した規格化係数とみなせる。また式($\ref{eq:rhomle}$)から$\hat{\rho_t}$の$t$に依存しない定数部分を除き、適当な数$10^3, 10^6$を掛けた式($\ref{eq:rpkm}$)は、よく知られたMortazaviらのRPKM（1Kbあたりミリオンリードあたりのリード数）の定義になる。すなわち、素朴にRPKMを使っていても、マルチヒットの影響を考えなければ、$\rho_t$の最尤推定量（の定数倍）を転写産物の相対定量値として採用していることに等しい。ただし、実効長を用いなければ最尤推定量とならないことには注意が必要である。

RPKM/FPKMの落とし穴：TPMのススメ

こちらの論文やPachter氏自身が講演やブログで何度も触れていることだが、上記RPKM/FPKMはたしかに$\rho_t$の定数倍ではあるものの、その定数は実験依存だと注意喚起している。

Although abundances in FPKM are proportional to the relative abundances $\hat{\rho}_t$ the proportionality constant is experiment specific.
“Stories from the Supplement” from the Genome Informatics meeting 11/1/2013

つまり、同一サンプル内のRPKMの大小比較はRNAの濃度の特定の定数倍と考えて問題ないが、サンプル間比較のときには注意が必要ということである。これは以下のとおり簡単に示せる。式($\ref{eq:rhomle}$)より、

\[\begin{equation} \hat{\rho}_t = X_t \cdot \frac{10^3}{\tilde{l}_t} \cdot \frac{10^6}{N} \left( \sum_{r \in T} X_t \cdot \frac{10^3}{\tilde{l}_t} \cdot \frac{10^6}{N} \right)^{-1} = \frac{RPKM_t}{\sum_{r \in T} RPKM_r} \end{equation}\]

となる。これはすなわち、

\[\begin{equation} RPKM_t = \hat{\rho}_t \sum_{r \in T} RPKM_r \end{equation}\]

長さで補正するRP“K”Mであるがゆえ、全体の転写産物のうち、短い転写産物（ウェイト大）と長い転写産物（ウェイト小）へのリードの乗り方のバランスが異なれば、当然、異なるサンプル間で$\rho_t$に変化がなくても、定数は変わってしまう。つまり、FPKM/RPKMは転写産物の相対量（濃度のようなもの）を表す適切な指標ではないことに注意が必要である3。そこで、トータルRNA中の濃度として解釈可能なTranscripts Per Million (TPM)の使用が推奨されている。

\[\begin{eqnarray} TPM_t &=& 10^6 \cdot \rho_t \\ &=& 10^6 \cdot \frac{RPKM_t}{\sum_{r \in T} RPKM_r} \end{eqnarray}\]

これなら濃度$\rho_t$同士の比較になるので問題ない。ちなみに一部の転写産物の占領によって割合$\rho_t$そのものが影響を受けるようなケースは、サンプル間正規化と呼ばれる手法(e.g., TMM, geometric normalization/median-of-ratio)で補正される。補正してしまえば、このFPKMの定数倍問題は結果的に回避される。

マルチヒットを考慮したモデル

以降は、基本モデルである式($\ref{eq:likfun}$)の尤度関数をアップグレードしていく。今回の条件は、基本モデルからマルチヒットを考慮するという点のみ変更する。ただし、ややゆるやかな制約を設け、同一転写産物上に2箇所以上マルチヒットしないこととする。

多項分布タイプの生成モデル

さっそくだが、Xingらの提案したこのタイプの尤度関数は以下である。

\[\begin{equation} \label{eq:Xing} \mathcal{L}(\boldsymbol\alpha) = \prod_{i=1}^N \left( \sum_{k=1}^K y_{ik} \frac{\alpha_k}{\tilde{l}_k} \right) \end{equation}\]

ここで、$K=|T|$、また$y_{ik}$は、compatibility matrixと呼ばれる$N \times K$の行列$\mathrm Y = \left( y_{ik} \right)$の要素であり、$y_{ik} = 1$になるのは$i \in F_k$のときだけで、それ以外は$y_{ik} = 0$とする。ちなみに、ここでの添字は$i \in F, k \in T$であることに注意する。

意味するところは見たままで、式($\ref{eq:Xing}$)のカッコ内は、リード$i$を共有（マルチヒット）する転写産物$k$についてだけ、リードの取得確率の和をとったものである。和を取る際に$y_{ik}$が効いて、候補の転写産物だけがセレクトされる。各々のリードの取得確率がわかったので、すべてのリードについての取得確率の積をとったものが式($\ref{eq:Xing}$)の尤度関数である。

ただし、ここでは、複数の転写産物にマップされたリードは必ずいずれかのものであるという前提を置いている。前述のややゆるやかな制約が「1つのリードは転写産物のいずれかのもの」という事象の背反性を保障する限りで、素直に確率の和をとってしまって問題ない。

マルチヒットは同値関係

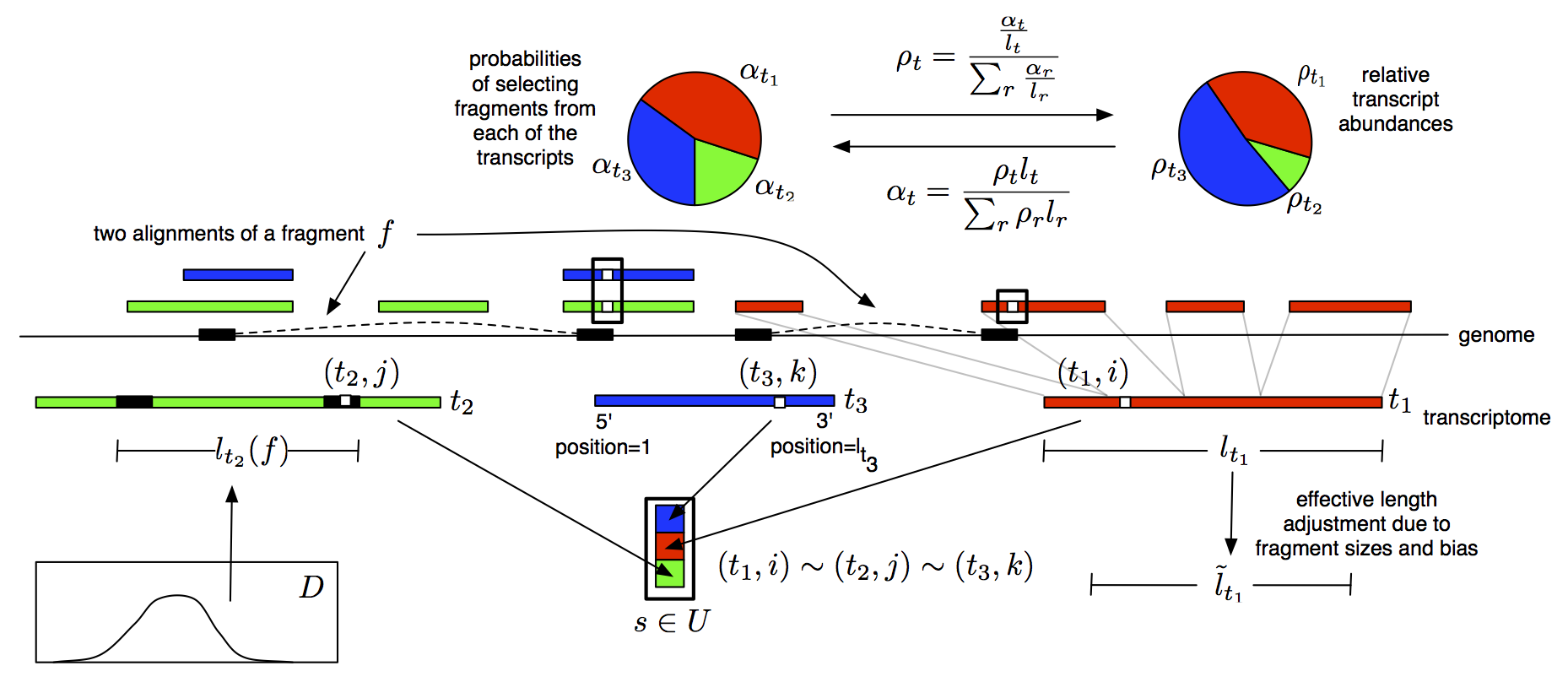
以下、この先必要な記法について、ややカタい方法で定義しておく。

転写産物$t$とその上の位置を示す添字$i$のペアの集合を$\mathcal{T}=\{(t,i)\ \mid \ t \in T, i \in \{1,\ldots,l_t\}\}$とする。$\mathcal{T}$のふたつの要素$(t,i)$および$(u,j)$の両者にマップされるリードが存在するとき、$(t,i) \sim (u,j)$と書く。このときの関係$\sim$は、以下の条件を満たすため、同値関係である。

  • 反射律
    $x \sim x$
  • 対称律
    $x \sim y$ ならば $y \sim x$
  • 推移律
    $x \sim y, y \sim z$ ならば $x \sim z$

ちなみに、数塩基のミスマッチを許したマッピングでは推移律を満たさないので一般に同値関係ではない4。同値関係であれば、集合$\mathcal T$を同値類に分割できる。それら同値類全体の集合を$U=\mathcal T / \sim$と定義する。このように定義することで、同値類のひとつ$s \in U$を指定すれば、特定のマルチヒット可能な位置の集合に対応させる記法が使える。また、$s \in U$にマップされるリードの部分集合を$F_s \subseteq F$と定義する。この定義もまた、$F$の分割を与えている。

同値類で塗り分けて分割された集合のイメージ

ポアソン分布タイプのモデル

Jiangらの提案した生成モデルでは、$F$が$s$にマップされる個数は、以下の平均パラメータ$\lambda_s$を持つポアソン分布に従うとしている。

\[\begin{equation} \label{eq:poismean} \lambda_s = \sum_{k=1}^K c_{sk} \frac{\kappa_k}{\tilde{l}_k} \end{equation}\]

ここで、site-transcript compatibility matrixを${\bf C}=(c_{sk}), s \in U, k \in T$とする。式$(\ref{eq:Xing})$のときと同様に、ある$s \in U$について、$\exists i \ \ s.t.\ (t,i) \in s$のとき$c_{st} = 1$で、それ以外では$c_{st}=0$となる特定の$t$だけを選ぶための係数である。またここで、急に$\kappa_k$という正体不明なパラメータが導入されたが、これはrate parameterと呼ばれ、転写産物$k$のリード数の期待値になっている。その期待値は、$\kappa_t = N\alpha_t$として見積もられたものと考えると納得がいく5。実際に、式($\ref{eq:poismean}$)の中で置き換えてみる。

\[\begin{equation} \lambda_s = N \sum_{k=1}^K c_{sk} \frac{\alpha_k}{\tilde{l}_k} = N \cdot \mathrm P ( f \in F_s ) \end{equation}\]

この形から、$\lambda_s$は特定のマルチヒットとなる対象の位置の集合$s$のいずれかに3’-endがマップされるリードの数$|F_s|$の期待値であると分かる。係数$c_{sk}$との絡みでもう少し噛み砕けば、

\[\begin{equation} \mathrm P(k \in T,(k,i)=s) = \mathrm P(k \in T) \mathrm P ((k,i) \in s \mid k \in T) = \alpha_k \cdot \frac{1}{\tilde{l}_k} \end{equation}\]

が、$c_{sk}=1$の意味するところである。すなわち、$s$を含んでいる特定の転写産物$k$を選り分けたうえで、$(k,i) \in s$となる確率を見ている。あとは簡単で、$F_s$に含まれるリード数を確率変数$X$とおいて、それがパラメータ$\lambda_s$のポアソン分布に従うとしたとき、$X$が実現値$X_s = |F_s|$をとる確率$\mathrm P(X=X_s)$のすべての$s \in U$について積をとれば、ポアソン分布タイプのマルチヒットを考慮した生成モデル（尤度関数）が得られる。

\[\begin{equation} \label{eq:Jiang} \mathcal{L}(\boldsymbol\kappa) = \prod_{s \in U} \left( \frac{e^{-\lambda_s}\lambda_s^{X_s}}{X_s!}\right) \end{equation}\]

多項分布タイプとポアソン分布タイプは同一

じつは、Xing($\ref{eq:Xing}$)とJiang($\ref{eq:Jiang}$)のモデルは、見た目や発想は違えど、結果として同じ最尤推定量を与える同一のモデルである。思い切って、式($\ref{eq:Jiang}$)の定数部分を無視するところから始める。

\[\begin{eqnarray} \mathcal{L}(\boldsymbol\kappa) &\propto& \prod_{s \in U} \lambda_s^{X_s}\\ &=& \prod_{s \in U} \left( N \sum_{k=1}^K c_{sk} \frac{\alpha_k}{\tilde{l}_k}\right)^{X_s}\\ &\propto& \prod_{s \in U} \left( \sum_{k=1}^K c_{sk} \frac{\alpha_k}{\tilde{l}_k}\right)^{X_s}\\ &=& \prod_{i = 1}^N \left( \sum_{k = 1}^K y_{ik} \frac{\alpha_k}{\tilde{l}_k}\right)\\ \end{eqnarray}\]

以上で、ふたつのモデルが同一であることが証明された。最後の式変形は、各同値類$s$の要素数$X_s$個単位の確率の積でまとめてから総積を取るか、リードのひとつ分ずつ確率の総積とっているかの違いであり、$U$が$F$の分割を与えていることから保障される。

一般化RNA-Seq定量モデル

単純なモデルで考慮しなかった、現実的に生じる様々なバイアスについて考慮した、一般化RNA-Seqt定量モデルについて概略を説明する。

一般化定量モデルパラメータの概略　

以下、各種バイアスを表現する新しい重みパラメータを導入する。

  • $w_{\frac{i}{l_t}}$
    転写産物の種類に関係なく生じる、断片の3’開始位置（$[0,1]$の相対位置）のバイアス
  • $u_{(t,i)}$
    特定の転写産物$t$の塩基配列等に起因して生じる断片の3’開始位置$i$におけるバイアス
  • $v_{(t,i)}$
    5’位置に生じる同バイアス

上記いずれも$\leq 1$の実数であり、バイアスがない場合は恒等的に$1$である。また、断片長のばらつきも考慮する。

  • D
    断片長の分布
  • $l_t(f)$
    断片$f$の転写産物$t$における長さ

本項の目的は、このモデルの尤度関数を得るために、特定のひとつの配列断片$f$（ペアエンド）が取得される確率$\mathrm{P}(f^{3’}=(t,i),l(f)=l_t(f))$を得ることである。言い換えれば、ひとつの断片$f$に対応する$t$のうちの断片の3’-endの配置$i$が決まり、かつ、5’の位置（断片長$l_t(f)$）が決まる確率（同時確率）の表現を得ることである。

$t$が決まった時、$f$の3’-endの位置$f^{3’} = (t,i)$を得る確率

単純なモデルでは、この確率分布は一様であった$1/\tilde{l}_t$が今回はバイアスおよび断片長の不確定性から非一様な分布となる。まず、すでに断片$f$に対応する$t$が決まっているときの、その断片の3’の位置$f^{3’}$が$t$の$i$番目に位置する条件付き確率を考える。

\[\begin{equation}\label{eq:f3prime} \mathrm{P}(f^{3'} = (t,i) \mid f \in F_t) = \frac{w_{\frac{i}{l_t}}\cdot u_{(t,i)} \cdot \sum_{j=1}^{i-1}\frac{D(i-j)}{\sum_{k=1}^{i-1}D(i-k)} v_{(t,j)}}{\tilde{l}_t} \end{equation}\]

ここでは、3’の位置だけが決まっていて、まだ5’の位置、すなわち長さ$l(f)$は未定であることに注意する。これは、分子の$\sum$の項は5’の取りうるすべての位置についての重みの総和であることからわかる。また、$D(i-j)/\sum_{k=1}^{i-1}D(i-k)$という部分は、3’の位置$(t,i)$が決まったとき、$t$は最大$i$の長さを持つので、断片長の分布$D$の条件付き分布$D(x \mid x \leq i)$を使って、$1,\ldots,i$の範囲で5’の各々の位置取りについて重み付けを行っていると考えればよい。また、この場合の分母の実効長$\tilde{l}_t$は、以下で定義される。

\[\begin{equation} \tilde{l}_t \quad = \quad \sum_{i} \left( w_{\frac{i}{l_t}}\cdot u_{(t,i)} \cdot \sum_{j=1}^{i-1}\frac{D(i-j)}{\sum_{k=1}^{i-1}D(i-k)} v_{(t,j)}\right) \end{equation}\]

この実効長は、$t$上のすべて位置$i$の重み（すべての重みの積）の総和であり、確率を$1$にするための規格化定数になっている。このモデルの$\tilde{l}_t$は、断片長の分布$D$と各バイアスによる重みから決まる、転写産物$t$の上でのリードの3’が取得可能な位置の総数の期待値というイメージを持つのが分かりやすいかもしれない。

$f^{3’} \in (t,i)$が決まり、かつ、断片長が$l_t(f)$となる同時確率

まず、$f^{3’}=(t,i)$となる確率を考える。ただしこの$f^{3’}=(t,i)$には、$f \in F_t$かつその3’が$t$の$i$番目に位置するという意味をあらわしていることに注意する。この確率は、さきほどの式($\ref{eq:f3prime}$)の条件付き確率に$\mathrm P(f \in F_t)$を掛けるだけで求めることができる。

\[\begin{eqnarray} \mu_{(t,i)} &:=& \mathrm{P}(f^{3'} = (t,i), f \in F_t)\\ & = & \mathrm{P}(f \in F_t) \mathrm{P}(f^{3'} = (t,i) \mid f \in F_t) \\ & = & \alpha_t \frac{w_{\frac{i}{l_t}}\cdot u_{(t,i)} \cdot \sum_{j=1}^{i-1}\frac{D(i-j)}{\sum_{k=1}^{i-1}D(i-k)} v_{(t,j)}}{\tilde{l}_t} \end{eqnarray}\]

また、$t$と$f^{3’}=(t,i)$が決まっているとき、$l(f)=l_t(f)$となる確率は、式($\ref{eq:f3prime}$)と同様に$D$を使って以下のように書ける。

\[\begin{equation} \zeta^f_{(t,i)} := \mathrm{P}(l(f) = l_t(f) \mid f^{3'}=(t,i), f \in F_t) = \frac{D(l_t(f)) v_{(t,i-l+1)}}{\sum_{j=1}^{i-1}D(i-j)v_{(t,j)} } \end{equation}\]

これらの２つの確率の積が、$t$、かつ、その位置$f^{3’} \in (t,i)$が決まり、かつ、断片長が$l_t(f)$となる同時確率となる。

\[\begin{eqnarray} \mathrm{P}(f^{3'} = (t,i),l(f)=l_t(f),f \in F_t) & = & \mu_{(t,i)} \zeta^f_{(t,i)}\\ & = & \alpha_t \frac{ u_{(t,i)} \cdot v_{(t,i-l+1)} \cdot w_{\frac{i}{l_t}} \frac{D(l_t(f))}{ \sum_{k=1}^{i-1}D(i-k) } }{\tilde{l}_t}. \end{eqnarray}\]

マルチヒット対象$s$の要素$(t,i) \in s$については確率$\mathrm{P}(f^{3’} = (t,i),l(f)=l_t(f))$の和をとり、あとはそれら$s \in U$のすべてについて総積をとったものが、尤度関数となる。

\[\begin{eqnarray} \mathcal{L}(\alpha)& = & \prod_{s \in U} \prod_{f \in F_s} \sum_{(t,i) \in s} e_{tf} \mathrm{P}(f^{3'}=(t,i),l(f)=l_t(f), f \in F_t)\\ & = & \prod_{s \in U} \prod_{f \in F_s} \sum_{(t,i) \in s} e_{tf} \mu_{(t,i)} \zeta^f_{(t,i)}\\ & = & \prod_{s \in U} \prod_{f \in F_s} \sum_{(t,i) \in s} \alpha_te_{t,f}\frac{1}{\tilde{l}_t} \frac{D(l_t(f))}{\sum_{k=1}^{i-1}D(i-k) } u_{(t,i)} v_{(t,i-l_t(f)+1)} w_{\frac{i}{l_t}} .\label{eq:genlik} \end{eqnarray}\]

ここで、$e_{tf}$は、前述のcompatibility matrixの要素$y_{tf} \in \{0,1\}$を一般化したもので、$f$が$t$に対して持つinsersion/deletionやミスマッチ塩基数により重みの決定される実数係数である。

一般化したモデルで説明したような各種のバイアス項を導入した定量モデルは、eXpressとして実装、公開されている。

Cufflinksのモデル

詳細な導出過程は論文にまかせるとして省略し、cufflinksの想定するRNA-Seqデータの尤度関数の概要のみ説明する。

\[\begin{equation} \left( \prod_{g \in G} \beta_g^{X_g} \right) \left( \prod_{g \in G} \left( \prod_{r \in R: r \in g} \sum_{t \in g} \gamma_t \cdot \frac{F(I_t(r))}{l(t)- I_t(r) + 1} \right) \right) \end{equation}\]

ここで、$g \in G$はある遺伝子座$G$に属するisoform $g$の集合をあらわしている。また、$X_g$はグループ$G$のトータルリード数、$R$はリード全体の集合、$I_t(r)$はペアエンドリードの長さ、$F$は断片長の分布（各長さに対する確率）をあらわしている。ここでのパラメータ群は、

\[\begin{equation} \beta_g = \sum_{t \in g} \alpha_t, \quad \gamma_t = \sum_{t \in g} \frac{\tau_t \tilde{l}(t)}{\sum_{u \in g} \tau_u \tilde{l}(u)}, \quad \tau_t = \frac{\rho_t}{\sum_{t \in g} \rho_t} \end{equation}\]

であり、$\beta$はlocusグループで前述の$\alpha$をひとまとめにしたもので、$\gamma$はある特定のlocus $G$で各isoformn $t$のタグが検出される確率($\alpha$のlocus限定版）だと思ってよい。

この尤度関数のポイントは、左の項のカッコの$\beta$と右側の$\gamma$はそれぞれ個別に最大化できるという点である。直感的には、locusを共有するisoformグループ内のリードの配分は一旦棚上げにしておいて、遺伝子単位で最適な$\beta$を算出し、各々の$\beta$の内訳を$\gamma$として推定するという手続きがとれる。ちなみに今までの議論と同じで、$\beta$の最尤推定量は$X_g/N$である。あとは、配分の最尤推定を$g$単位で行っていく。またlocusをまたがるマルチリードの問題がここでは無視されているが、Rescue method (-uオプション)を使うことで、最尤推定されたリード数の比率に応じてマルチリードを配分できる。

本稿で未解説のポイント

  • EMアルゴリズムによる尤度関数の数値的最適化法
  • 漸近理論を使ったcufflinksのパラメータ推定の信頼区間の導出

  1. 絶対量はRNA-seqデータからは原理的に不可知である ↩

  2. のちの発展形のモデルでは適宜最適なものを使う ↩

  3. Cuffdiff等サンプル間比較解析の際は、サンプル間の定数倍の違いを解消をgeometric normalization等でad-hocに調整しているため、結果的に定数倍の違いはキャンセルされる ↩

  4. $x \sim y,y \sim z$は$1$塩基ミスマッチを許容したマルチヒットの関係だとしても、$x$と$z$は$2$塩基ミスマッチとなる可能性がある ↩

  5. ここではPachter (2011)と異なるやりかたで説明している ↩